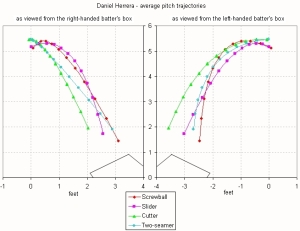
My article at Hardball Times on Danny Herrera’s screwball includes views of his pitch trajectories as seen from the right-handed and left-handed batter’s boxes.
I mentioned in the References section that I did some trigonometry to transform the coordinate system from plate view to batter’s box view.
Here is what I did.
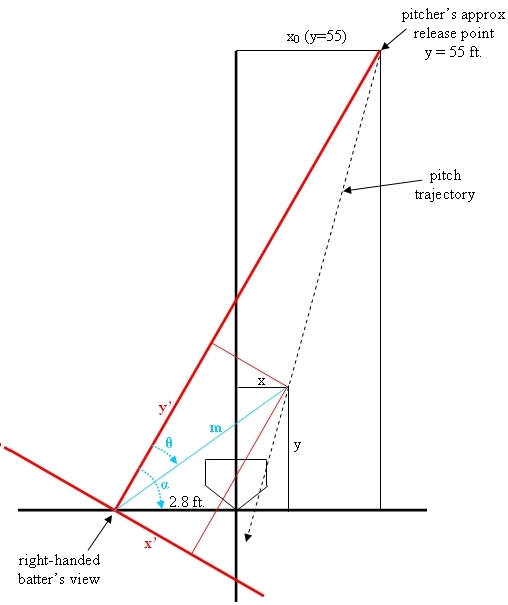
The pitch trajectory is shown as the dotted black line. Any point on the trajectory can be calculated using the initial position, velocity, and acceleration provided in the PITCHf/x data, along with the equations of motion. Only the x-y plane is shown above since no transformation was done to the z axis. The coordinates in the PITCHf/x coordinate space are x and y, shown in black.
The coordinates in the batter’s box view are x’ and y’, shown in red. The y-axis in the batter’s box view runs along a line from the batter’s head to the pitcher’s approximate release point (the average x value of his pitches at y = 55 feet). The x-axis in the batter’s box view is set perpendicular to this new y-axis.
The origin of the batter’s box view is offset 2.8 feet in the x direction from the origin in PITCHf/x coordinate space. I calculated 2.8 feet from the center of the plate as the approximate location of the batter’s head, based on a video frame capture in Marv White’s presentation at the PITCHf/x Summit. I chose not to offset the origin in the y direction for simplicity, although I also believe this does not introduce any significant inaccuracy. The batter’s head is typically within a foot or so of y=0.
First, I calculated the quantity m, the distance to the baseball, shown by the blue line. This distance m = sqrt ( y^2 + ( x + 2.8 ft)^2 ).
Next, I found the value of the angle alpha. The angle alpha = arctan ( 55 ft / ( x0 + 2.8 ft) ).
The angle (alpha – theta) = arctan ( y / ( x + 2.8 ft) ), which allows us to calculate the angle theta.
The angle theta = arctan ( 55 ft / ( x0 + 2.8 ft) ) – arctan ( y / ( x + 2.8 ft) ).
The batter’s box coordinates x’ and y’ can be found from the angle theta and the distance m. The new y’ = m * cos (theta), and the new x’ = m * sin (theta).
I am happy for you to use my method for batter’s view transformation if you provide attribution in the form of my name and/or a link to this website.
June 16, 2008 at 6:15 am
Great!
With your efforts, I can analyze many more things from pitch f/x data!
Thank you very much, Mr.Fast!
June 16, 2008 at 1:04 pm
I read your Hardball Times article and I was about to email you to ask for the details of the batter’s box transformation…and then I come here and there it is! Thanks a lot, this will be fun to play with.
June 17, 2008 at 10:22 am
what do you use for drawing these trajectories?
I got x’, y’ values, but still I cannot get the trajectories that I wanted.
Isn’t that the trajectory plotted by excel?
How did you merged 3 dimensional data into 2 dimensional plane?
June 17, 2008 at 11:33 am
Mike,
It *may* be interesting (or at least fun) to additionally impose a vanishing point. It might give it a more 3Dish feel.
June 17, 2008 at 11:42 am
RandoLL: those plots are just x’ plotted against z, I think. At least, I get similar results when I plot them that way. (Incidentally, it looks like these plots were done in R, not Excel.)
June 17, 2008 at 12:30 pm
Peter is correct, the plots are z versus x’.
I did the plots in Excel. I wish I were more facile with R than I am. I’ve dinked around in R a little bit, but I haven’t mastered it like I have Excel.
Ike, I thought about using a vanishing point, but I chickened out of doing the work to implement it. I definitely need to do something like that if I’m going to have the correct perspective around the plate and strike zone. You can see that there is an implied vanishing point in how I drew home plate, but the trajectories don’t reflect that, of course, and I didn’t draw a strike zone box because it doesn’t like right without that 3-D perspective.
June 20, 2008 at 4:49 pm
Mike – This is great stuff. It really adds to the “immersion” factor, getting a hitter’s-eye view.
July 21, 2009 at 1:35 pm
[…] of what Swarzak’s pitches look like coming in to a right-handed hitter, and to a lefty. See here for more on these […]
August 16, 2016 at 9:08 am
Can you tell me what the area in the outfield is called that is left green (in DC it is a green grass area) so the batter is able to pick up the ball from the pitcher’s hand?
Bruce